Математика – это один из самых популярных предметов, которые ученик изучает с самого начала своей школьной жизни. Среди множества задач, вопросы о треугольниках и четырехугольниках — это одни из самых часто задаваемых. Информация о средних линиях треугольника может пригодиться во многих задачах, связанных с нахождением периметра и площади треугольника.

Так что же такое средняя линия треугольника? Среднюю линию треугольника также называют «средним отрезком треугольника». Она представляет собой линию, соединяющую середины двух сторон треугольника. Интересно, что в треугольнике средняя линия всегда параллельна третьей стороне и составляет половину ее длины. Это свойство треугольника можно доказать с помощью теоремы о средней линии треугольника.

Средняя линия треугольника имеет массу полезных свойств. Например, с помощью средних линий треугольника можно разделить треугольник на четыре равные по площади треугольника. Также известно, что пересечение средних линий треугольника образует точку, которая делит каждую из средних линий в отношении 2:1. Это полезное свойство при решении задач о делении отрезка в заданном отношении.

Средняя линия треугольника также может быть использована для построения параллелограмма или трапеции, а также для поиска других часто встречающихся в геометрии фигур. Умение находить и использовать средние линии треугольника – это полезная и востребованная навык уже на начальном этапе изучения геометрии.

Что такое средняя линия треугольника и как ее определить?

Средняя линия треугольника имеет несколько важных свойств и способов определения. В геометрии она изучается из-за своей полезности и популярности.

Свойства средней линии треугольника:

• Средняя линия треугольника делит этот треугольник на две равные по площади части.
• Средняя линия треугольника является половиной длины соответствующей стороны.
• Если в треугольнике есть трапеция, то средняя линия параллельна и равна половине суммы оснований этой трапеции.
• Средняя линия треугольника всегда проходит через точку пересечения трех медиан треугольника, называемую центром масс треугольника.

Средняя линия треугольника – важный инструмент не только для умения находить средние значения, но и для решения задач в жизни. В математике она может пригодиться при изучении задач о разделении отрезка в заданном отношении.

Учебный урок посвященный средним линиям треугольника может помочь учащимся лучше понять эту тему и научиться применять ее в решении сложных задач. Он дает информацию о теореме о средних линиях треугольника, объясняет правила построения средних линий и предлагает решение практических задач.

Задачи и ответы по теме «Что такое средняя линия треугольника и как ее определить?»:

• Какие свойства имеют средние линии треугольника?
• Что такое средняя линия треугольника?
• Как определить среднюю линию треугольника?
• В каких случаях средняя линия треугольника параллельна стороне треугольника?
• Какие задачи можно решить при использовании средних линий треугольника?

Также средние линии применяются при изучении других фигур, например, при изучении параллелограмма и четырехугольников. Изучение средних линий имеет значимость и применение не только в геометрии, но и в различных областях жизни.

Определение, понятие, значение

Средняя линия является полезной информацией о треугольнике, поскольку через ее свойства можно получить много полезной информации о треугольнике и задачах, связанных с ним. Средняя линия треугольника всегда параллельна основанию треугольника и делит его площадь пополам. Также она является одной из восьми линий в геометрии треугольника, и ее свойства часто исследуются в классе. Знание и умение работать с средними линиями треугольника может пригодиться в математике и в жизни.

Изучение средних линий треугольника

Изучают средние линии треугольника, как часть изучения геометрии треугольников. Они являются одним из важных признаков треугольника и могут быть задаваемые через стороны треугольника. Равными средними линиями треугольника являются также средние линии параллелограмма и трапеции.

Задачи и решения

Средние линии треугольника имеют множество применений в различных математических задачах и решениях. Они могут быть использованы для нахождения площади треугольника, для решения задач на геометрические конструкции и теоремы, а также для представления треугольника в других геометрических фигурах. Познание свойств и использование средних линий треугольника поможет в решении различных задач и ответе на вопросы, связанные с этой темой.

Свойства средней линии треугольника

Средняя линия треугольника есть половина суммы длин его сторон. Это свойство может быть полезно при решении задач связанных с нахождением периметра или площади треугольника.

Теорема о средней линии треугольника: средняя линия параллельна третьей стороне и равна половине длины этой стороны.

Средние линии треугольника также могут быть полезны при изучении параллелограммов: в параллелограмме средняя линия равна половине диагонали.

Средняя линия треугольника является одной из часто задаваемых вопросов в геометрии, и ее свойства могут быть полезны при решении разнообразных задач. Она также может пригодиться в повседневной жизни для решения популярных задач, связанных с нахождением массы или делением предметов на равные части.

Средние линии треугольника имеют также ряд свойств, которые могут быть полезны в учебном процессе. Например, средние линии треугольника пересекаются в одной точке, называемой центром тяжести треугольника. Это свойство может быть полезно при изучении геометрии.

Таким образом, информация о свойствах средней линии треугольника является полезной и может быть использована при решении различных задач, как в математике, так и в повседневной жизни.

Способы построения средней линии треугольника

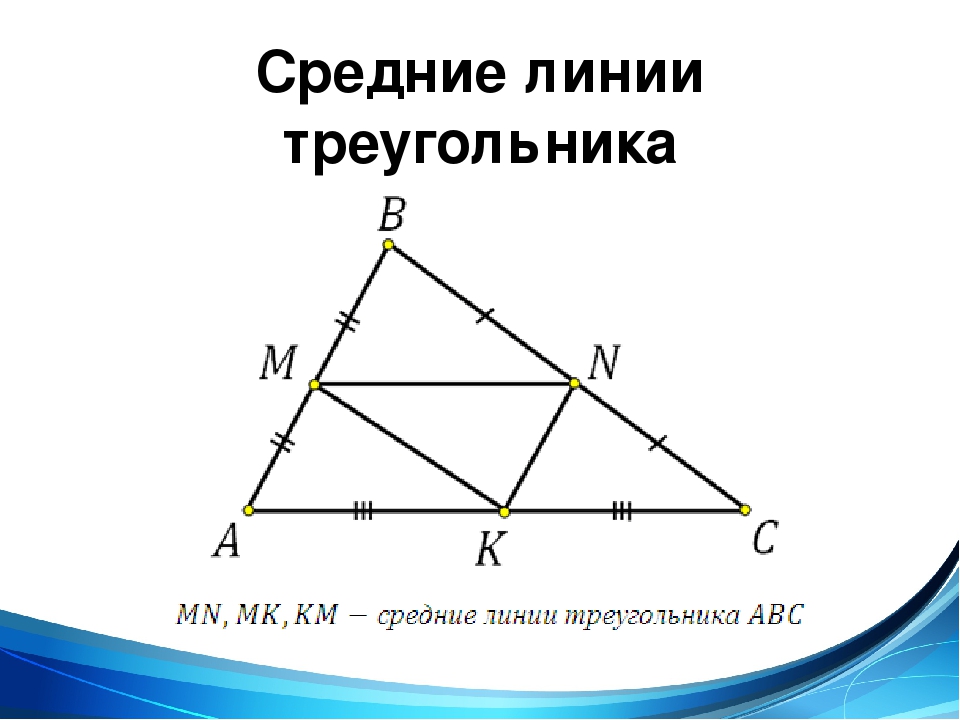
Первый способ основан на теореме о средних линиях треугольника. Согласно этой теореме, среднюю линию треугольника можно построить, соединив середины двух его сторон. Для этого необходимо найти середины сторон треугольника путем деления их на две равные части. Затем проводится линия, соединяющая эти середины, и она будет средней линией треугольника.

Второй способ построения средней линии треугольника основан на свойствах параллелограмма. Согласно этим свойствам, средняя линия треугольника также является медианой и высотой параллелограмма, который имеет те же стороны, что и исходный треугольник. Следовательно, можно построить параллелограмм на основе треугольника и провести его медиану, которая будет совпадать с средней линией треугольника.

Третий способ построения средней линии треугольника основан на свойстве трапеции. Если середины двух параллельных сторон трапеции соединить прямой линией, то она будет являться ее средней линией. Пользуясь этим свойством, можно построить трапецию, основаниями которой будут две стороны треугольника, а средней линией — средняя линия треугольника.

Таким образом, существует несколько способов построения средней линии треугольника. Знание этих способов и теорем, связанных с средней линией треугольника, может быть полезным при решении задач и вопросов, связанных с геометрией и математикой в жизни и в классе.

Способы с использованием компаса и линейки

В математике средняя линия треугольника играет важную роль. Она есть линия, соединяющая середины двух сторон треугольника. Поскольку эта линия делит треугольник на две равные части, она также называется медианой.

Существует несколько способов построения средней линии треугольника с использованием компаса и линейки. Вот некоторые из них:

1. Построить треугольник и использовать компас и линейку для построения отрезков, соединяющих середины сторон треугольника.
2. Построить треугольник, а затем провести серединные перпендикуляры к его сторонам. Точка пересечения этих перпендикуляров будет серединой треугольника и, следовательно, будет лежать на средней линии.
3. Построить треугольник, отметить середины его сторон и использовать компас и линейку для построения отрезка, соединяющего эти середины.

Важно отметить, что средняя линия треугольника параллельна каждой из его сторон и равна половине длины стороны. Это свойство можно использовать для решения различных задач и построений в геометрии.

В классах по геометрии ученики изучают различные вопросы, связанные с средней линией треугольника. Это популярная тема, так как знание и умение находить средние линии треугольника может пригодиться в жизни и полезно для решения задач и задачам, связанных с треугольниками и другими четырехугольниками.

Вот некоторые из наиболее популярных теорем и свойств, связанных с средней линией треугольника:

• Средняя линия треугольника делит его площадь на две равные части.
• Середины всех сторон треугольника и точка их пересечения лежат на одной прямой — средней линии треугольника.
• Для параллелограмма средняя линия равна половине диагонали.
• Средняя линия треугольника равна половине суммы длин двух других сторон.
• Для трапеции средняя линия параллельна основанию и равна полусумме длин оснований.

Это лишь основная информация о средней линии треугольника и ее свойствах. Если тебя интересует эта тема, смотри еще больше материала по геометрии и изучай задачи, связанные с этой важной линией треугольника.

Способы с использованием графического программного обеспечения

Если мы зададимся вопросом о том, нахождение средней линии треугольника — это полезная информация, которая может пригодиться нам при решении задач. Например, средняя линия обладает свойством быть параллельной третьей стороне треугольника и равной половине ее длины. Это свойство может помочь нам в решении задач на нахождение периметра или площади треугольника. Также, она делит треугольник на два равных по площади треугольника.

Существует несколько способов построения средней линии треугольника с использованием графического программного обеспечения. Один из них — с использованием графических инструментов, доступных в программе. Мы можем нарисовать треугольник, использовав для этого инструменты для построения линий и углов. Затем, мы можем построить середины двух сторон треугольника и соединить их линией, чтобы получить среднюю линию.

Еще одним способом является использование функций программного обеспечения, которые позволяют найти середины сторон треугольника автоматически. Например, многие программы имеют функцию поиска середины отрезка или автоматического построения середины линии. Такие функции могут значительно упростить процесс построения средней линии и сэкономить время.

Способ	Описание
Использование графических инструментов	Рисуем треугольник и соединяем середины сторон линией
Использование функций программного обеспечения	Используем функции поиска середины отрезка или автоматического построения серединной линии

О делении отрезка на равные части

В уроках геометрии ученики часто изучают свойства треугольника и изучают такие понятия, как «средняя линия треугольника», «пополам», «средняя точка». Зачем же учить все это в школе и в классе?

Основанием для изучения этой темы является теорема о средних линиях треугольника. Согласно этой теореме, средние линии треугольника – это линии, соединяющие середины его сторон. Такое определение даёт ученикам представление о том, что умение находить среднюю линию треугольника может быть полезным в жизни для решения различных задач.

Один из способов нахождения средней линии треугольника – это деление стороны пополам. Если мы имеем треугольник ABC, то среднюю линию треугольника, проходящую через сторону BC, можно получить, разделив эту сторону пополам. Такое деление поможет нам найти точку на этой линии, которая делит сторону пополам.

С помощью средних линий можно также делить отрезки на равные части. Если нужно разделить отрезок, например AB, на n равных частей, то надо построить среднюю линию, проходящую через этот отрезок, и разделить ее на n равных отрезков. Так мы получим несколько отрезков, равных между собой.

Еще один способ нахождения средней линии треугольника – это через площади треугольника. Если точка D – середина стороны BC, то площадь треугольника ABC будет равна сумме площадей треугольников ABD и ACD. Это позволяет найти точку D на средней линии треугольника ABC.

Помимо деления отрезков на равные части, средние линии находят применение и в изучении параллелограмма, трапеции и других четырехугольников.

Таким образом, знание свойств и способов нахождения средней линии треугольника является важным умением в геометрии и математике. Изучают эмпирические задачи, популярные в жизни и в научных исследованиях. Ученики научатся решать задачи, где необходимо находить среднюю линию треугольника, или делят другие отрезки на равные части.

Значимость данной темы в геометрии и математике позволяет ученикам переходить к изучению других тем, которые с ней связаны.

Методы и алгоритмы деления отрезка

Средняя линия треугольника — это линия, которая соединяет середины его сторон. Такая линия часто используется в классе для изучения свойств треугольника. Она также является полезной информацией при решении задач на нахождение площади треугольника или других частей треугольника.

Существует несколько способов нахождения средней линии треугольника. Один из них основан на теореме о делении отрезка в отношении 1:2. Согласно этой теореме, средняя линия треугольника проходит через середину основания треугольника и параллельна двум другим сторонам треугольника. Также можно использовать свойства трапеции или параллелограмма для нахождения средней линии треугольника.

Способы построения средней линии треугольника:

1. Взять отрезок, соединяющий середины двух сторон треугольника, и построить его продолжение через середину третьей стороны.

2. Найти середину одной из сторон треугольника с помощью пересечения двух середин других сторон.

3. Использовать свойства трапеции или параллелограмма для нахождения средней линии треугольника.

Знание и применение методов и алгоритмов деления отрезка является важным элементом изучения геометрии. Решая задачи на нахождение средней линии треугольника или четырехугольника, можно научиться логическому мышлению, анализу и построению решений. Это навыки, которые пригодятся в жизни и других математических предметах.

Что такое «средняя линия треугольника»? Задачи на нахождение средней линии треугольника часто задают в школьной программе по геометрии и математике. Она является важным признаком, так как средняя линия треугольника делит каждую сторону на две равные части. Почему средние линии треугольника также являются параллельными? Если точка делит отрезок на две равные части, то эта точка называется серединой отрезка. Средняя линия треугольника соединяет середины его сторон, следовательно, она параллельна сторонам треугольника. Это свойство средней линии треугольника обусловлено свойствами параллелограмма.